Lesson 2: Enlargement and Similar Figures

🟦 Introduction

Hi there, smart thinker! 👋 Today we’re exploring Enlargement and Similar Figures. These ideas help us understand how shapes grow or shrink while keeping the same form. Have you ever zoomed in on a photo and noticed that even though it gets bigger, the image doesn’t change shape? That’s enlargement! When two shapes have the same shape but different sizes, they are called similar figures. Let’s dive in and explore how to work with them in math!

🟩 Key Concepts and Explanations

🔹 What is Enlargement?

Enlargement means increasing or decreasing the size of a figure while keeping the same shape. Every point on the figure moves away from (or toward) a fixed point called the centre of enlargement.

• If the scale factor is greater than 1, the image becomes bigger.
• If the scale factor is between 0 and 1, the image becomes smaller.

Rule: Multiply all lengths (sides) by the scale factor.

Formula:

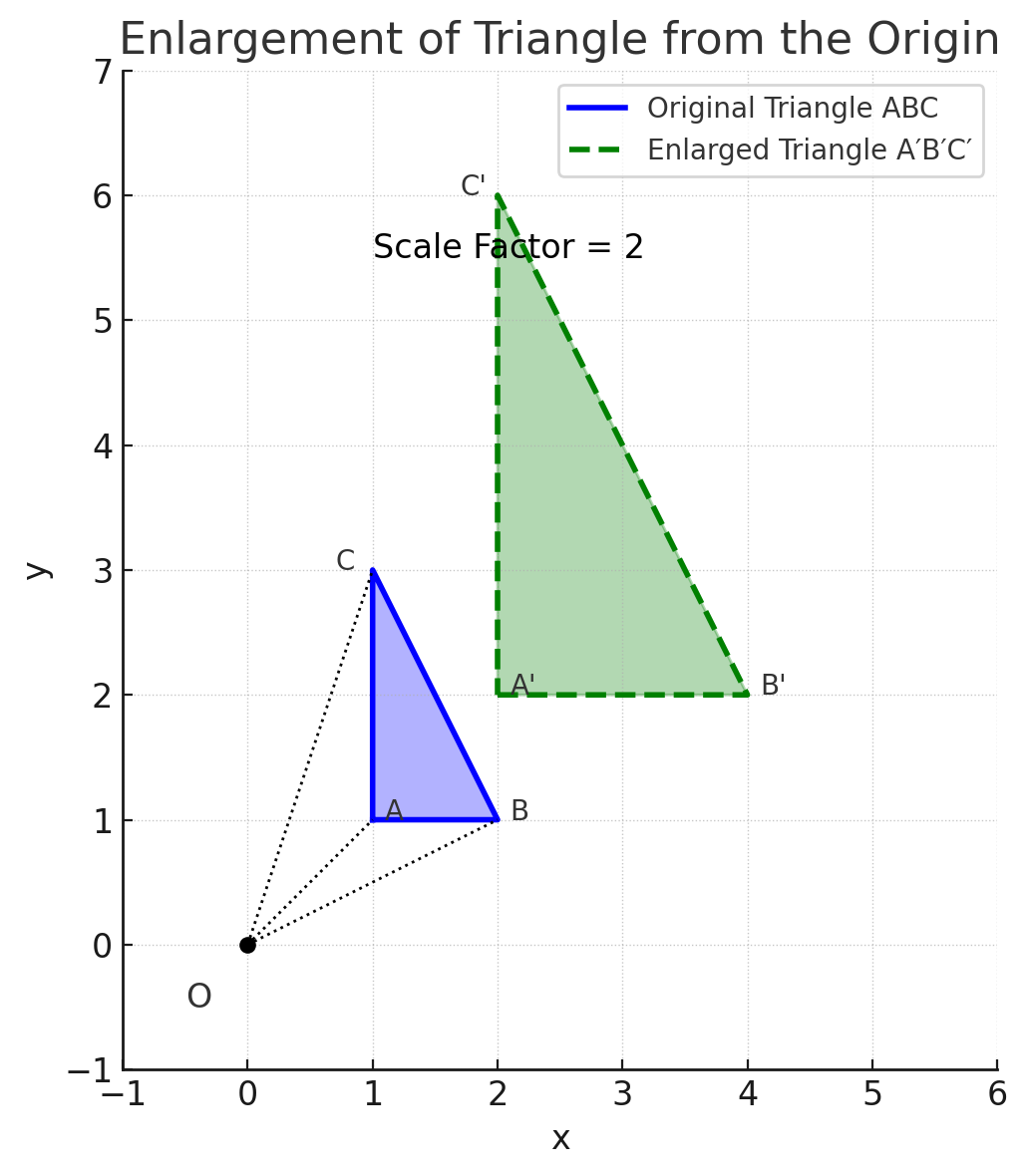
Placeholder for Diagram: [Insert Diagram Here: Triangle enlarged 2× from the origin]

🔹 What Are Similar Figures?

Similar Figures have the same shape but not necessarily the same size. Their angles are equal, and their corresponding sides are in the same ratio.

Examples of similar figures:

• Two triangles with equal angles but different side lengths
• A photo and its zoomed-in version

To check for similarity:

1. Compare corresponding angles — they must be equal.
2. Compare the ratios of corresponding sides — they must be the same.

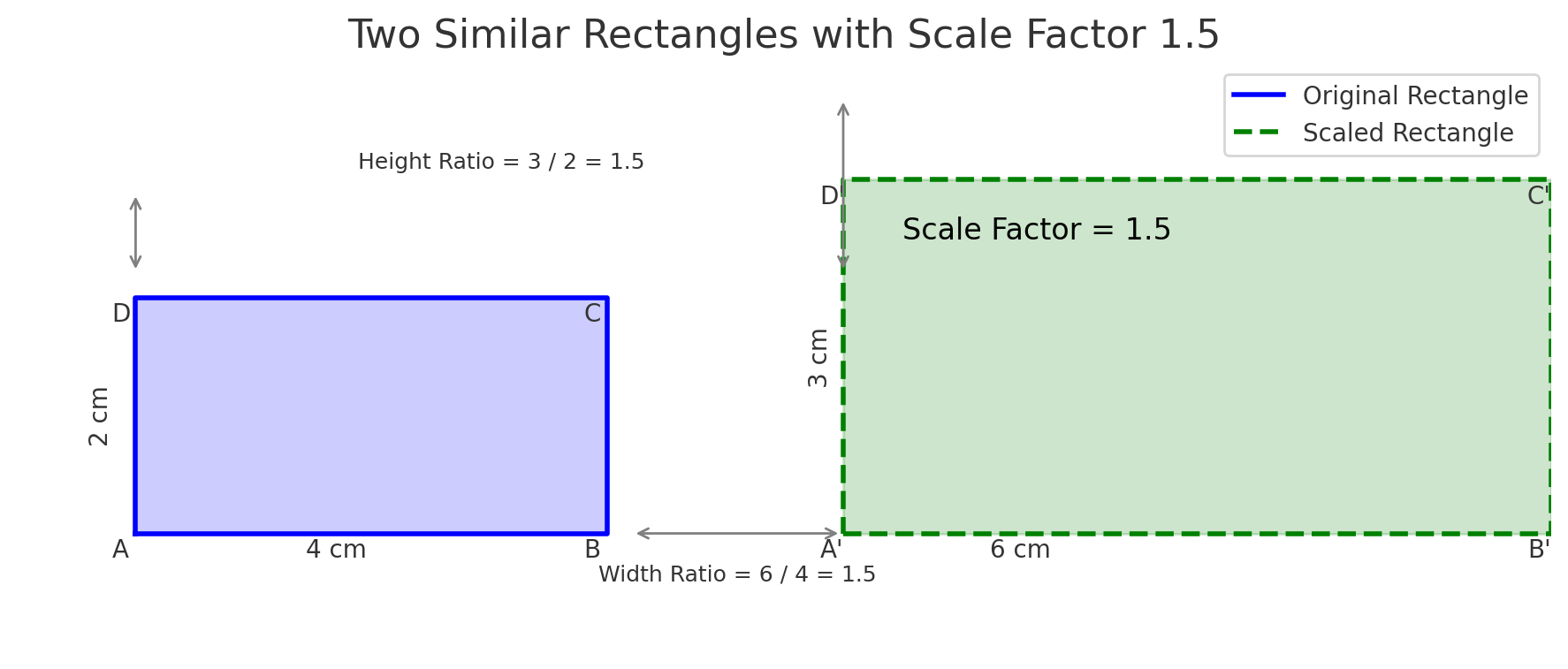
Placeholder for Diagram: [Insert Diagram Here: Two similar rectangles, one scaled by factor 1.5]

🔹 What Is a Scale Factor?

A scale factor tells us how many times larger or smaller the image is compared to the original shape.

If the original side is 4 cm and the image side is 8 cm:

Scale factor = image ÷ original

🟨 Sample Problem Walkthroughs

Sample 1: Enlargement Using a Scale Factor

The side of a square is 3 cm. If it is enlarged by a scale factor of 4, what is the new side length?

Solution:

Answer: 12 cm

Sample 2: Determining the Scale Factor

Two rectangles are similar. One has a side of 6 cm, and the other has a side of 15 cm. What is the scale factor?

Solution:

Answer: The second rectangle is 2.5 times larger.

Sample 3: Identifying Similar Figures

Triangle A has sides 4 cm, 6 cm, and 8 cm. Triangle B has sides 6 cm, 9 cm, and 12 cm. Are they similar?

Solution:

• Compare side ratios:
• 

All ratios are the same → Yes, they are similar.

🟨 Practice Exercises

Section A: Enlargement

1. Enlarge a triangle with sides 2 cm, 3 cm, and 4 cm by a scale factor of 3. What are the new side lengths?
2. The image of a line is 20 cm long. If the original line was 5 cm, what is the scale factor?

Section B: Similar Figures

1. Are the rectangles with sides (6 cm, 4 cm) and (9 cm, 6 cm) similar?
2. Circle A has a radius of 3 cm and Circle B has a radius of 7 cm. Are they similar?

Section C: Mixed Problems

1. The side of a square becomes 10 cm after enlargement. If the scale factor is 2.5, what was the original side?
2. Two similar triangles have corresponding sides 5 cm and 12.5 cm. What is the scale factor?

✅ Answers and Explanations

• Section A:
  1. 6 cm, 9 cm, 12 cm
  2. Scale factor = 20 ÷ 5 = 4
• Section B:
  1. Yes. Ratios: 6:9 = 2:3, 4:6 = 2:3 → Same ratio
  2. Yes. All circles are similar (same shape, different sizes)
• Section C:
  1. Original = 10 ÷ 2.5 = 4 cm
  2. Scale factor = 12.5 ÷ 5 = 2.5

🔁 Recap

Today, you learned about Enlargement — growing or shrinking figures using a scale factor — and Similar Figures, which keep their shape but may differ in size. We used real-life examples, diagrams, and formulas to understand how transformations affect size and proportion.

🪞 Reflection Prompt

Can you think of something in your daily life that shows enlargement or similarity? Maybe a map, a photo, or a drawing? How would you describe the scale factor used?