Lesson 1: Rigid Motion – Translation, Reflection, Rotation

🟦 Introduction

Hello, brilliant learner! 👋 In this exciting lesson, we will explore how shapes can move without changing size or shape. When you shift your chair, flip a playing card, or turn a steering wheel, you are performing actions just like the transformations we study in Mathematics! These movements are called Rigid Motions. Let’s learn about Translation, Reflection, and Rotation together, with real-life examples, easy formulas, diagrams (to be inserted later), and fun practice!

🟩 Key Concepts and Explanations

🔹 What is Rigid Motion?

Rigid Motion is when a shape moves from one position to another without changing its size or shape. The distance between every pair of points stays the same. That means no stretching, no shrinking, no bending — just pure movement!

🔹 Translation

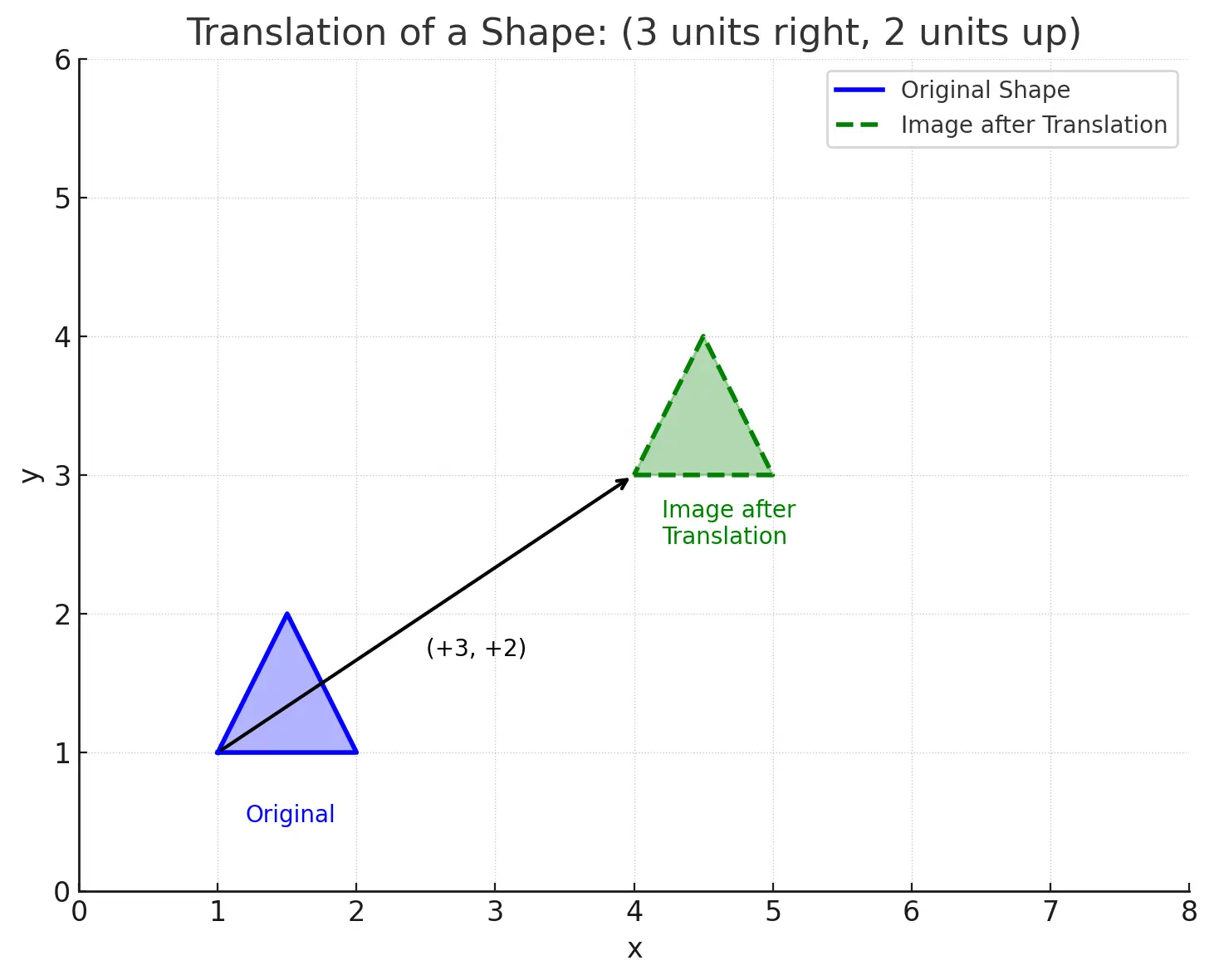
Translation moves every point of a figure the same distance in the same direction. Think of it like sliding!

Key Points about Translation:

• Shape stays the same ✅
• Size stays the same ✅
• Direction stays the same ✅

Example 1: Moving a chess piece straight across the board.

Example 2: Shifting your schoolbag from your desk to the next desk without lifting it up.

Rule: To translate a point (x, y) by (a, b), the new coordinates become:

🔹 Reflection

Reflection flips a figure across a line, creating a mirror image.

Key Points about Reflection:

• Each point and its image are the same distance from the mirror line.
• Figures face opposite directions.

Example 1: Your reflection in a bathroom mirror.

Example 2: Folding a paper and having both sides match exactly.

Common Reflection Rules:

• Reflection over the x-axis:
• Reflection over the y-axis:

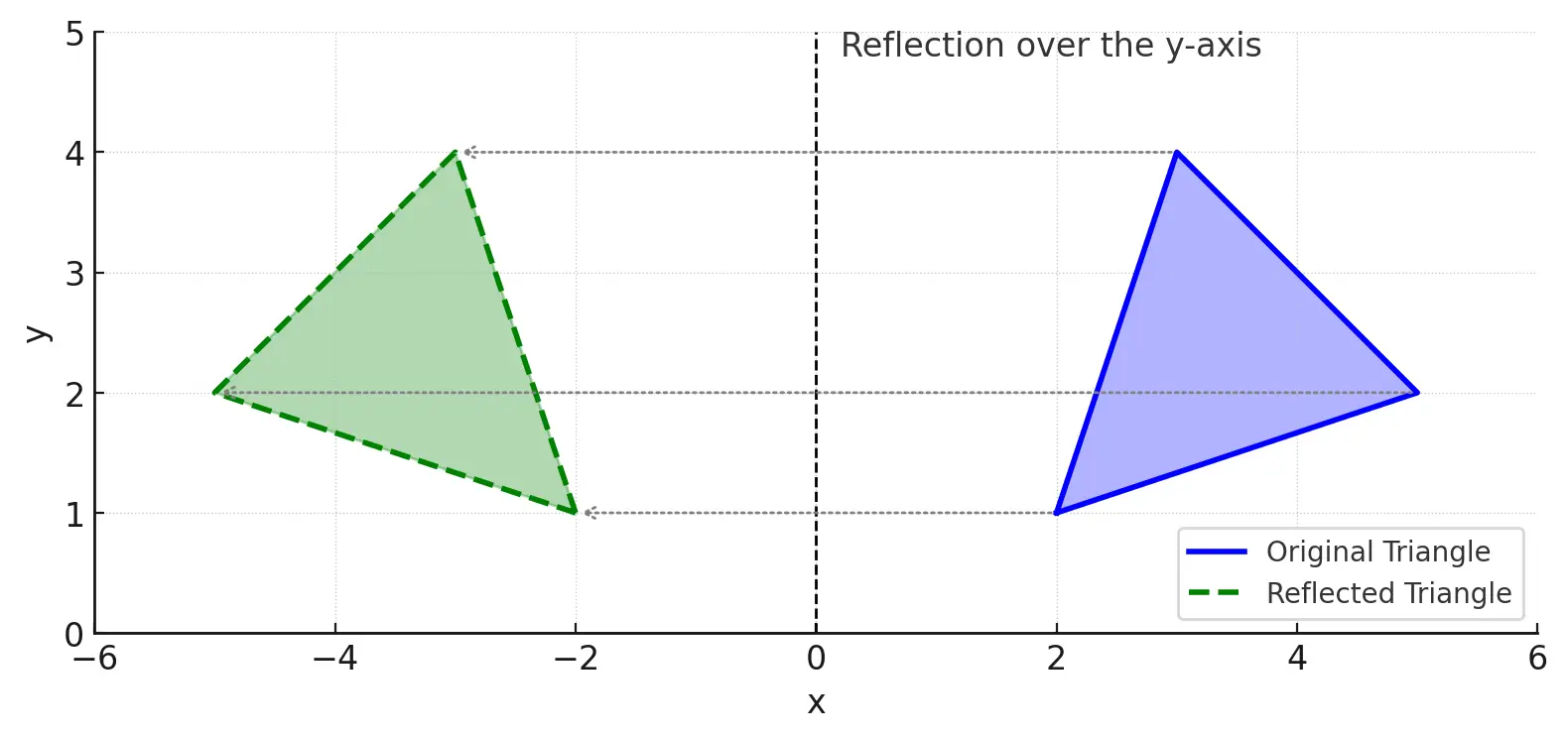
Placeholder for Diagram: [Insert Diagram Here: A triangle reflected over the y-axis]

🔹 Rotation

Rotation turns a figure around a fixed point called the center of rotation.

Key Points about Rotation:

• Shape stays the same ✅
• Size stays the same ✅
• Angle of turn is measured in degrees (90°, 180°, 270°)

Example 1: Rotating the hands of a clock.

Example 2: Twisting a bottle cap open.

Common Rotation Rules (about the origin):

• 90° counterclockwise:
• 180°:
• 90° clockwise:

Placeholder for Diagram: [Insert Diagram Here: Rotation of a point around the origin]

🟨 Sample Problem Walkthroughs

Sample 1: Translation

Translate P(3, -2) by 2 units left and 5 units up. Find the new coordinates.

Solution:

• Left means subtract 2 from x:
• Up means add 5 to y:

Answer: (1, 3)

Sample 2: Reflection

Reflect Q(-5, 2) over the x-axis.

Solution:

• Reflection over x-axis: change the sign of y.
• New coordinates: (-5, -2)

Sample 3: Rotation

Rotate R(0, 4) 90° clockwise about the origin.

Solution:

• 90° clockwise: (x, y) → (y, -x).
• So (0, 4) becomes (4, 0).

🟨 Practice Exercises

Section A: Coordinate Changes

1. Translate point A(5, 7) 3 units right and 2 units down. Find the new coordinates.
2. Reflect B(2, -6) over the y-axis. Find the new coordinates.
3. Rotate C(-2, 0) 180° about the origin. Find the new coordinates.

Section B: Fill in the Blanks

1. A __________ moves a shape by sliding without turning or flipping.
2. Reflection over the y-axis changes the __________ coordinate.
3. Rotation 90° counterclockwise swaps and changes __________ of the coordinates.

Section C: Matching

✅ Answers and Explanations

• Section A:
  1. (8, 5)
  2. (-2, -6)
  3. (2, 0)
• Section B:
  1. Translation
  2. x
  3. Order
• Section C:
  1. Translation
  2. Reflection
  3. Rotation

🔁 Recap

Today, we explored three powerful transformations:

• Translation (sliding),
• Reflection (flipping), and
• Rotation (turning).

All are rigid motions because they preserve size and shape. Mastering these transformations makes Geometry easier and more fun!

🪞 Reflection Prompt

Imagine you slide, flip, and rotate a paper shape. 🌟
Which movement feels the easiest for you? Which feels trickiest? Reflect on why!