Lesson 2: Operations on Sets

📚 Introduction

Now that you know what a set is, it’s time to learn what we can do with sets!
We can combine them, separate them, and find what’s common between them. These actions are called operations on sets.

In this lesson, we will learn how to:

• Find the union, intersection, and difference between sets
• Understand complements of sets
• Use Venn diagrams to show these operations

🧠 Key Concepts and Explanations

1. Union of Sets (A ∪ B)

The union of two sets is a new set that contains all the elements from both sets — without repeating any elements.

Symbol: ∪

Example:

• If A = {1, 2, 3} and B = {3, 4, 5}, then A ∪ B = {1, 2, 3, 4, 5}

2. Intersection of Sets (A ∩ B)

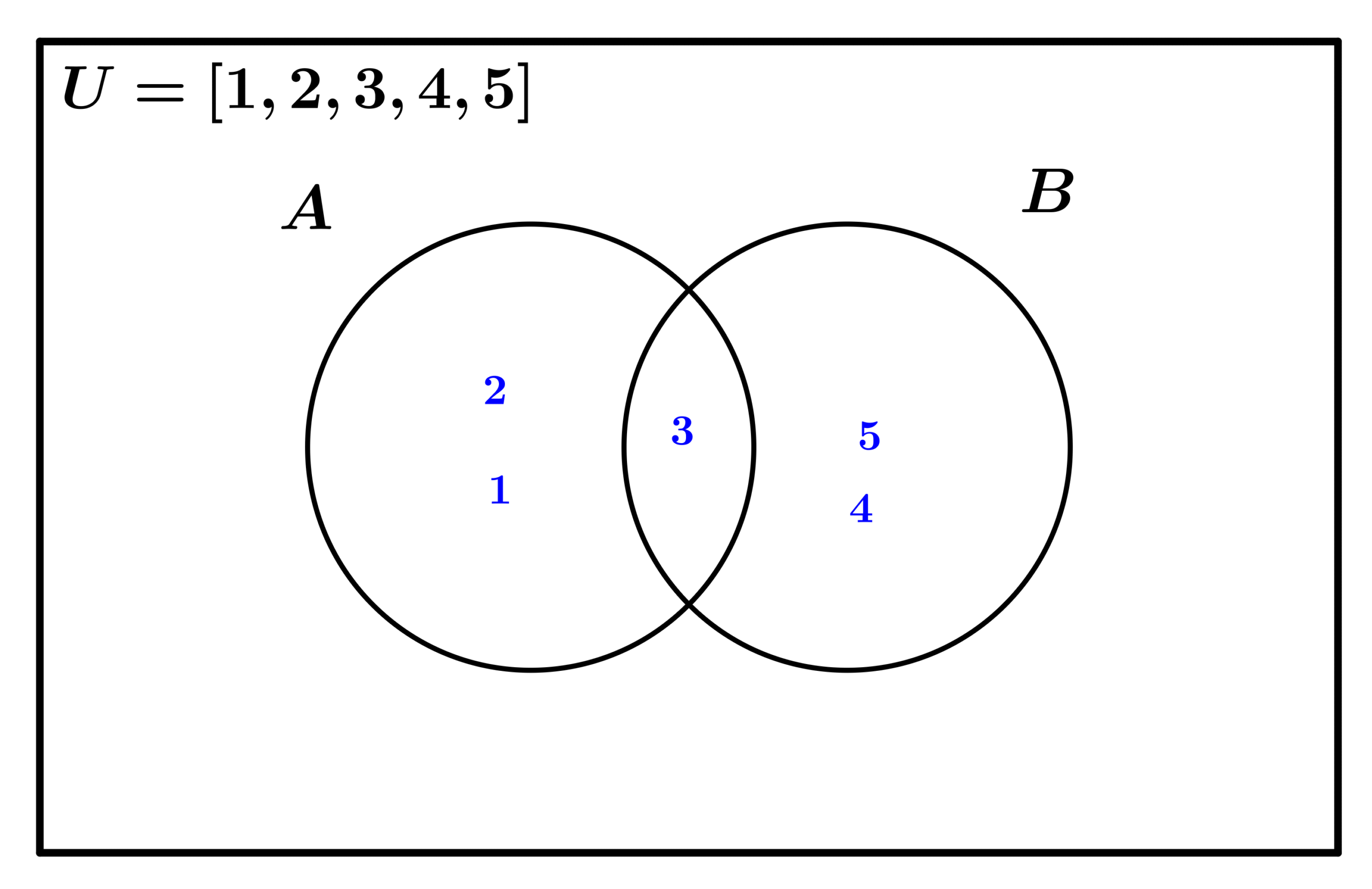
The intersection of two sets is a new set that contains only the elements that are common to both sets.

Symbol: ∩

Example:

• If A = {1, 2, 3} and B = {3, 4, 5}, then A ∩ B = {3}

3. Difference of Sets (A – B or B – A)

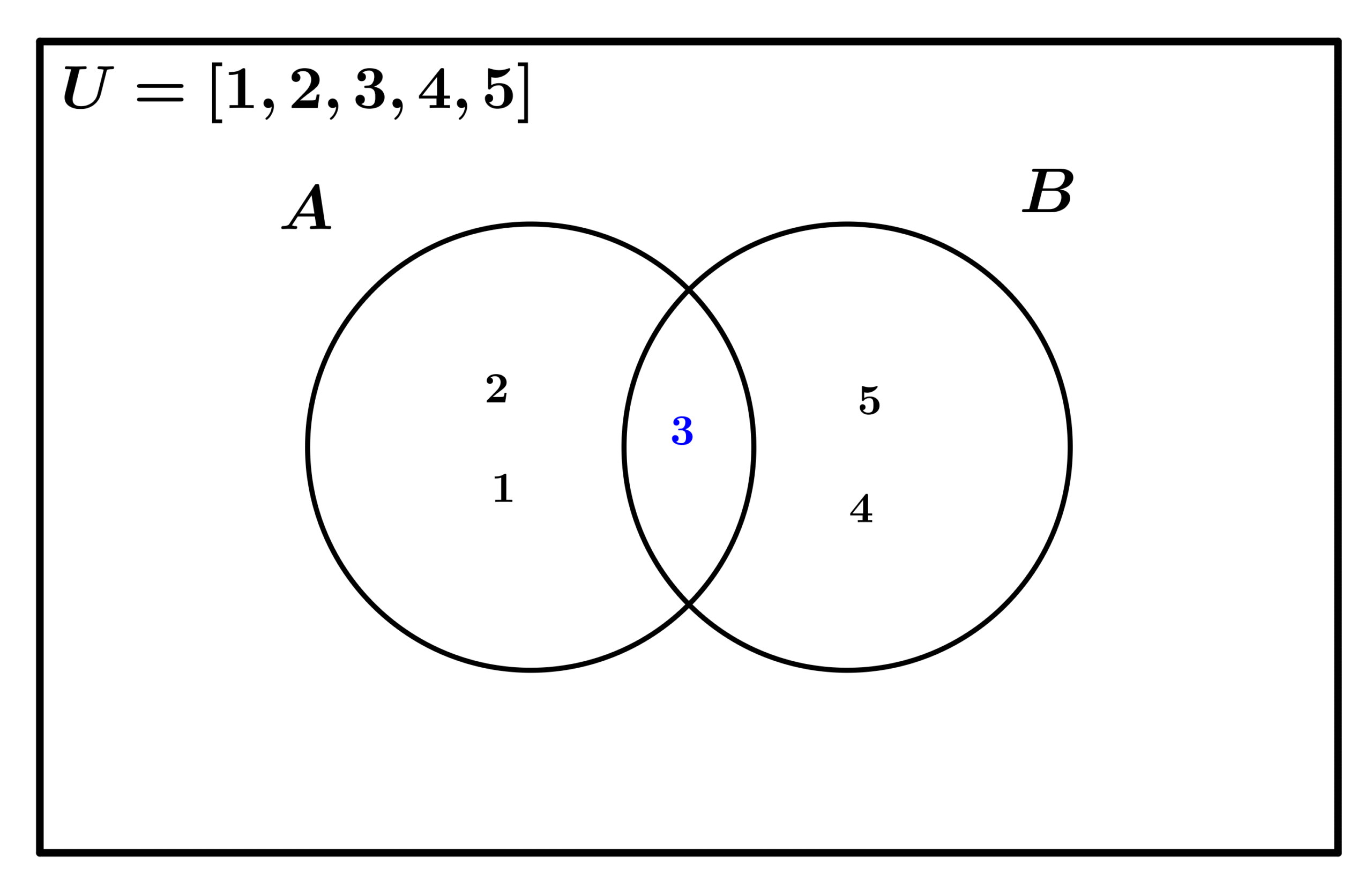
The difference of two sets A and B, written A – B, is the set of elements that are in A but not in B.

Example:

• If A = {1, 2, 3, 4} and B = {3, 4, 5}, then A – B = {1, 2}
• But B – A = {5}

4. Complement of a Set (A’)

The complement of a set A (written A’) is the set of all elements in the universal set that are not in A.

Example:

• Universal set U = {1, 2, 3, 4, 5, 6}
• A = {2, 4, 6}
• Then, A’ = {1, 3, 5}

📝 Sample Problem Walkthroughs

Example 1: Union

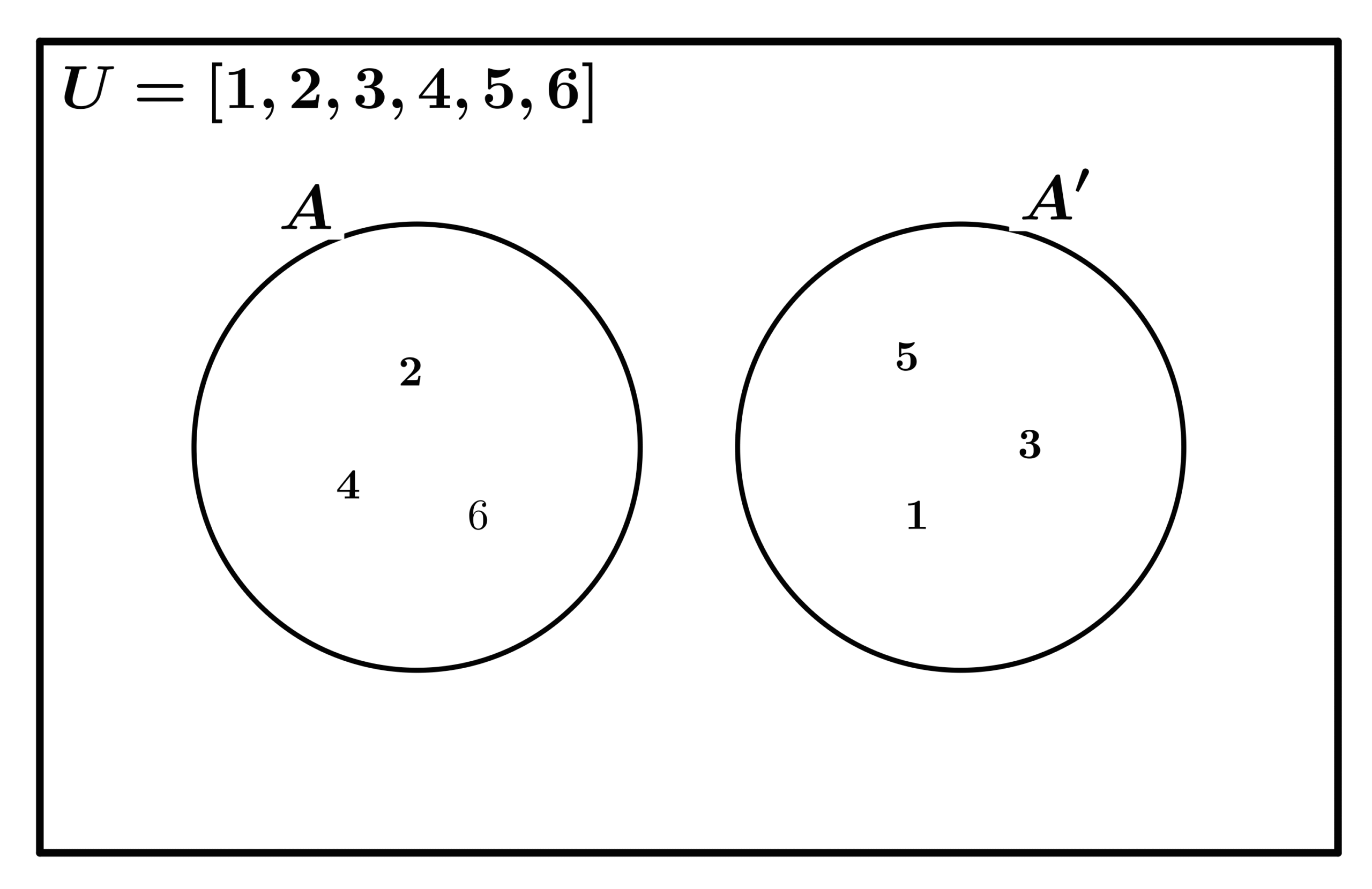
Question: Find A ∪ B if A = {apple, banana} and B = {banana, cherry}.

Solution: Combine all elements without repeating:

A ∪ B = {apple, banana, cherry}

Example 2: Intersection

Question: Find A ∩ B if A = {2, 4, 6, 8} and B = {4, 5, 6, 7}.

Solution: Common elements are {4, 6}.

Example 3: Difference

Question: Find A – B if A = {1, 3, 5, 7} and B = {3, 4, 5}.

Solution: Remove elements of B from A:

A – B = {1, 7}

Example 4: Complement

Question: If U = {a, b, c, d, e} and A = {a, e}, find A’.

Solution: Elements in U but not in A:

A’ = {b, c, d}

📝 Practice Exercises

Exercise 1:

Find the union of these two sets: P = {2, 4, 6} and Q = {5, 6, 7}.

Exercise 2:

Find the intersection of M = {cat, dog, lion} and N = {lion, tiger}.

Exercise 3:

Find the difference P – Q if P = {a, e, i, o, u} and Q = {e, i}.

Exercise 4:

If the universal set U = {1,2,3,4,5} and A = {2,3}, find the complement of A.

📝 Extra Challenge Problems

Challenge 1:

If X = {red, green} and Y = {green, blue, yellow}, list:

• X ∪ Y
• X ∩ Y
• X – Y

Challenge 2:

Draw Venn diagrams showing:

• Two overlapping circles for X and Y
• Highlight union, intersection, and difference areas

🔁 Recap

Today we learned four important operations on sets: union, intersection, difference, and complement.
We used examples and Venn diagrams to show how they work.
Mastering these operations helps in solving more advanced questions easily!

🪞