Shopping cart
Hello There!
Welcome to GattPrep, your Guide for Life and Learning
Hello there! 😊 In this lesson, we’ll explore the fascinating world of geometrical constructions and loci. You’ll learn how to draw accurate shapes and lines using only a ruler and a compass — just like mathematicians did before computers! Plus, we’ll see how loci (plural of locus) help us find all the possible places where something can be. Ready to draw, discover, and explore? Let’s begin!
Geometrical constructions are drawings made using only a ruler (to draw straight lines) and a compass (to draw arcs and circles). No measuring with protractors or scales — just pure accuracy through technique.
A locus is a set of points that satisfy a certain rule or condition. For example, all points that are the same distance from a fixed point form a circle — that’s a locus!
| Condition | Resulting Locus |
|---|---|
| Fixed distance from a point | A circle |
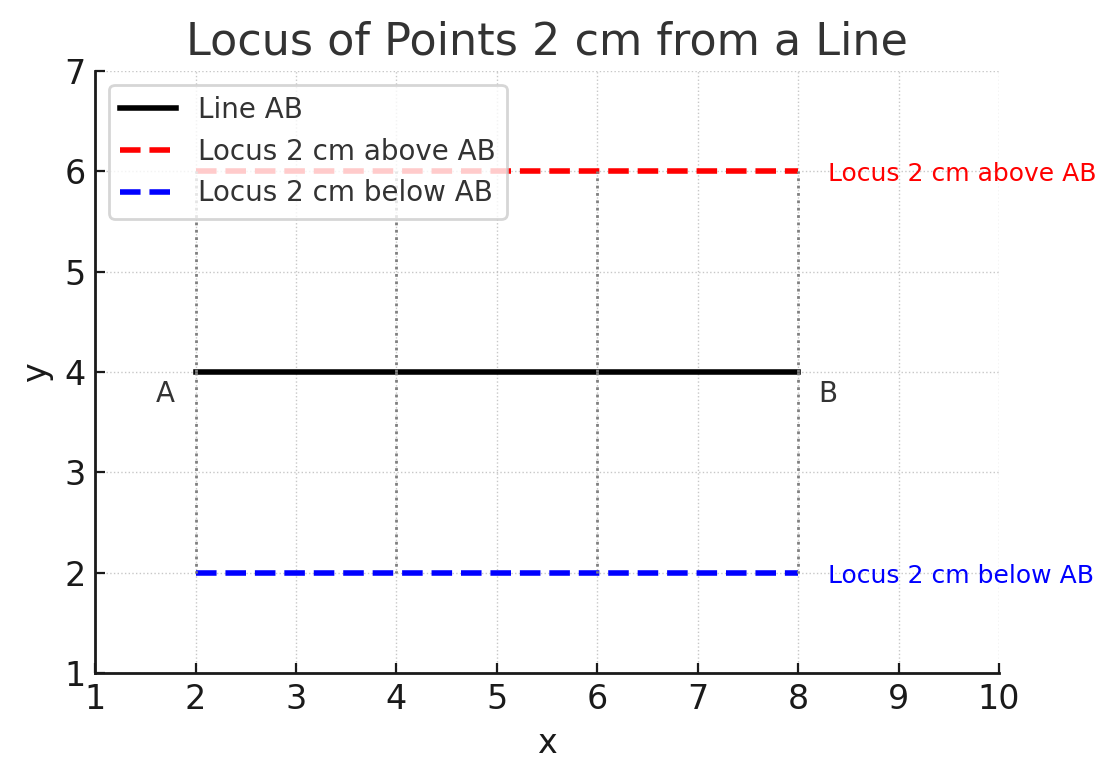
| Fixed distance from a line | Two parallel lines |
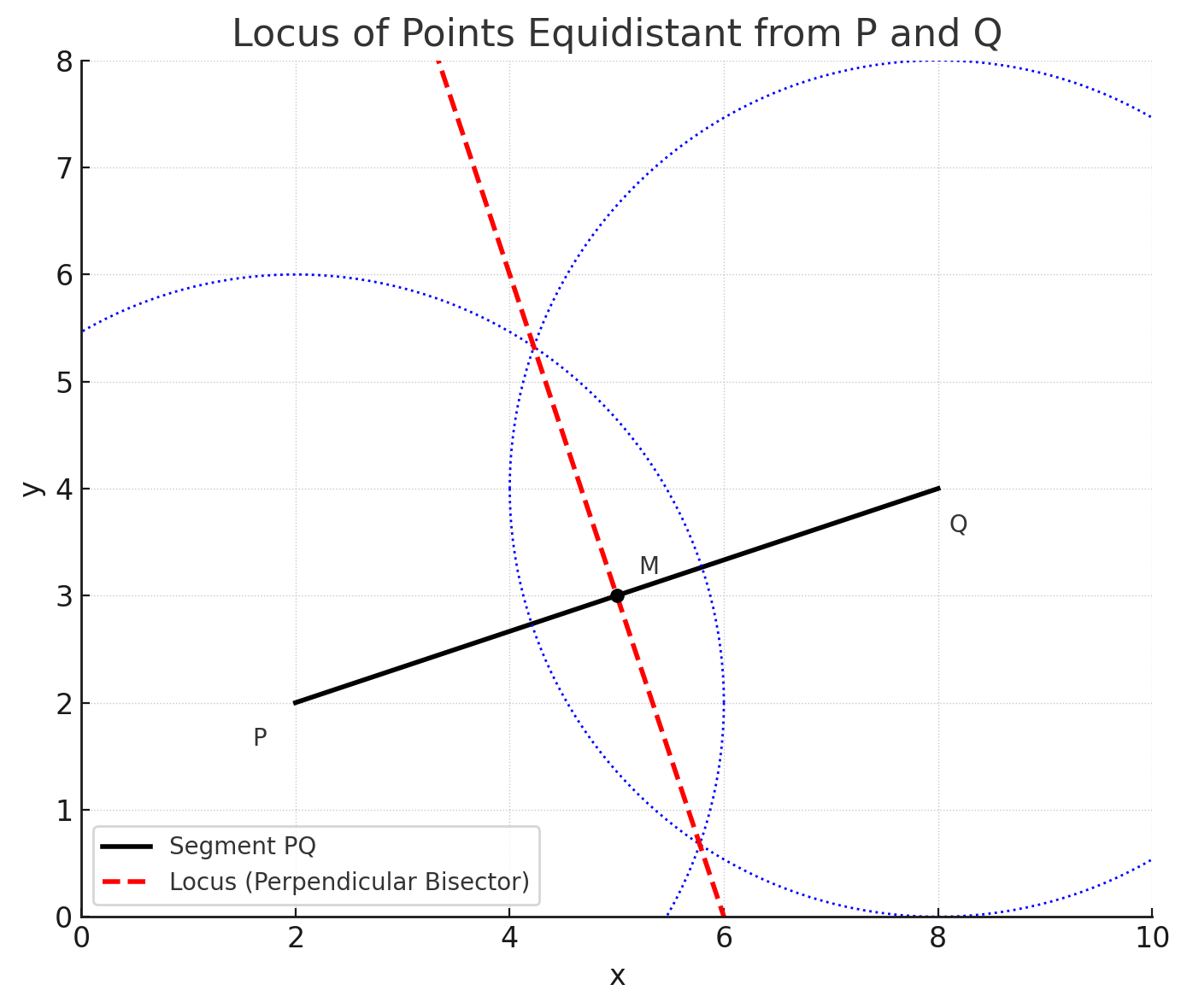
| Equal distance from two points | Perpendicular bisector of the line joining the two points |
| Equal distance from two lines | Angle bisector between the two lines |
Problem: Draw a line segment AB of length 6 cm and construct its perpendicular bisector.
Steps:
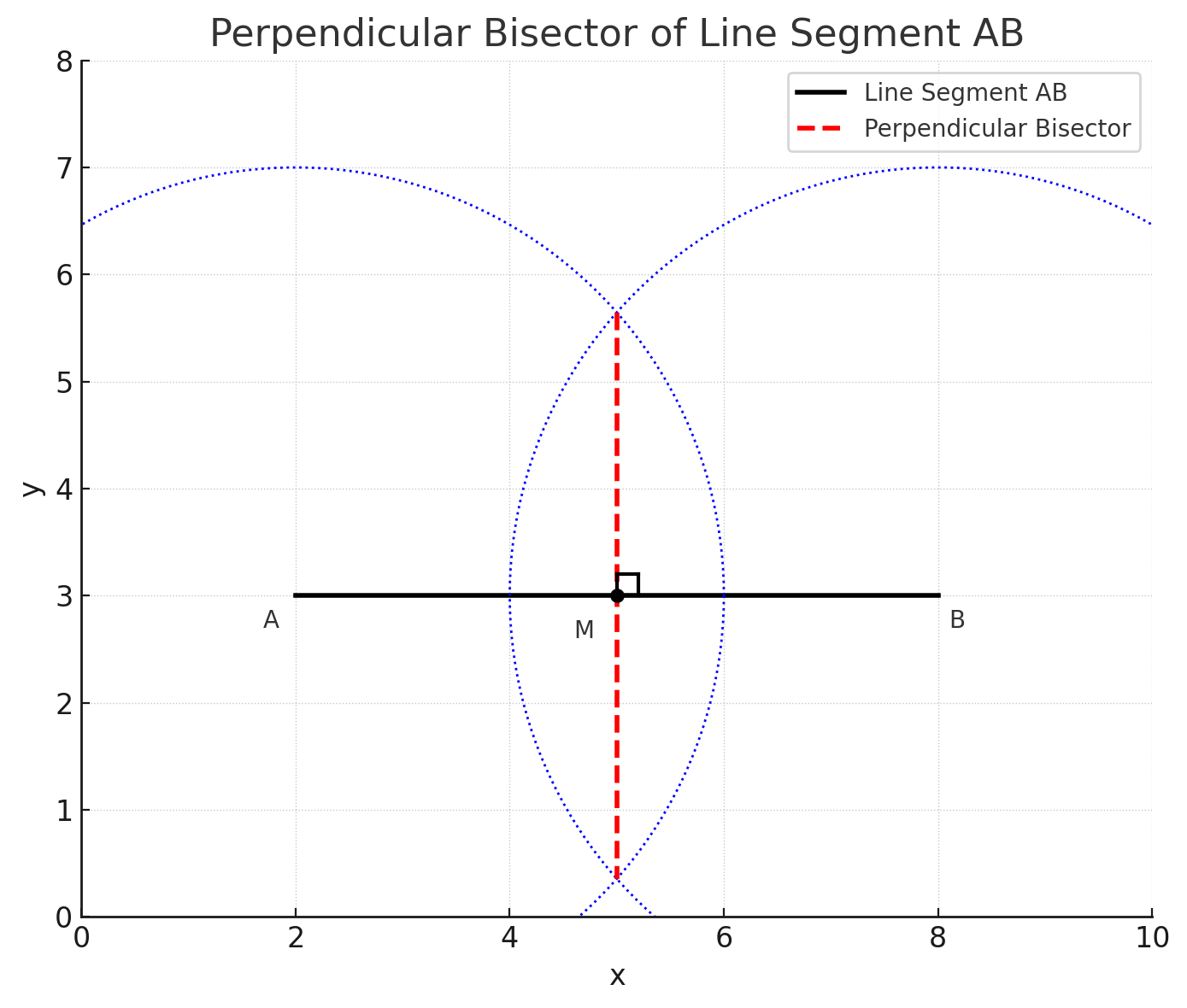
Problem: Given two points P and Q, construct the locus of points equidistant from P and Q.
Steps:
Steps:
Section A: Construction Tasks
Section B: Loci Identification
Section C: Matching
| Condition | Locus |
|---|---|
| Same distance from a fixed point | __________ |
| Same distance from a fixed line | __________ |
| Same distance from two points | __________ |
We’ve explored how to make precise constructions with a ruler and compass, including bisectors and triangle building. You’ve also discovered how loci describe the path of points that follow specific conditions — like equal distance from a point or line. These are powerful tools in geometry, useful in both exams and real-life planning!
Why do you think mathematicians prefer using ruler and compass for constructions? How might knowing loci help in real-life situations like engineering or landscaping?