Lesson 3: Linear Inequalities in One Variable – Solving and Graphing Solutions

🟦 Introduction

Welcome! Today, we move beyond solving equations into the world of inequalities. Inequalities are like equations, but instead of using an equals sign (=), they use signs like greater than (>), less than (<), greater than or equal to (≥), or less than or equal to (≤). You will learn how to solve inequalities step-by-step and even graph their solutions!

🧠 Key Concepts and Explanations

🔹 What is a Linear Inequality?

A linear inequality in one variable compares two expressions using an inequality sign instead of an equals sign.

Examples: x + 3 > 7, 2y – 4 ≤ 10, m/2 ≥ 5

🔹 Solving a Linear Inequality

To solve an inequality:

1. Solve it like a normal equation using addition, subtraction, multiplication, or division.
2. Important: If you multiply or divide by a negative number, you must reverse the inequality sign.

🔹 Inequality Signs and Their Meaning

➡️ Sample Problem Walkthroughs

🔹 Example 1: Solve and Graph

Solve: x + 5 > 12

Step 1: Subtract 5 from both sides:

🔹 Example 2: Solve with Multiplication

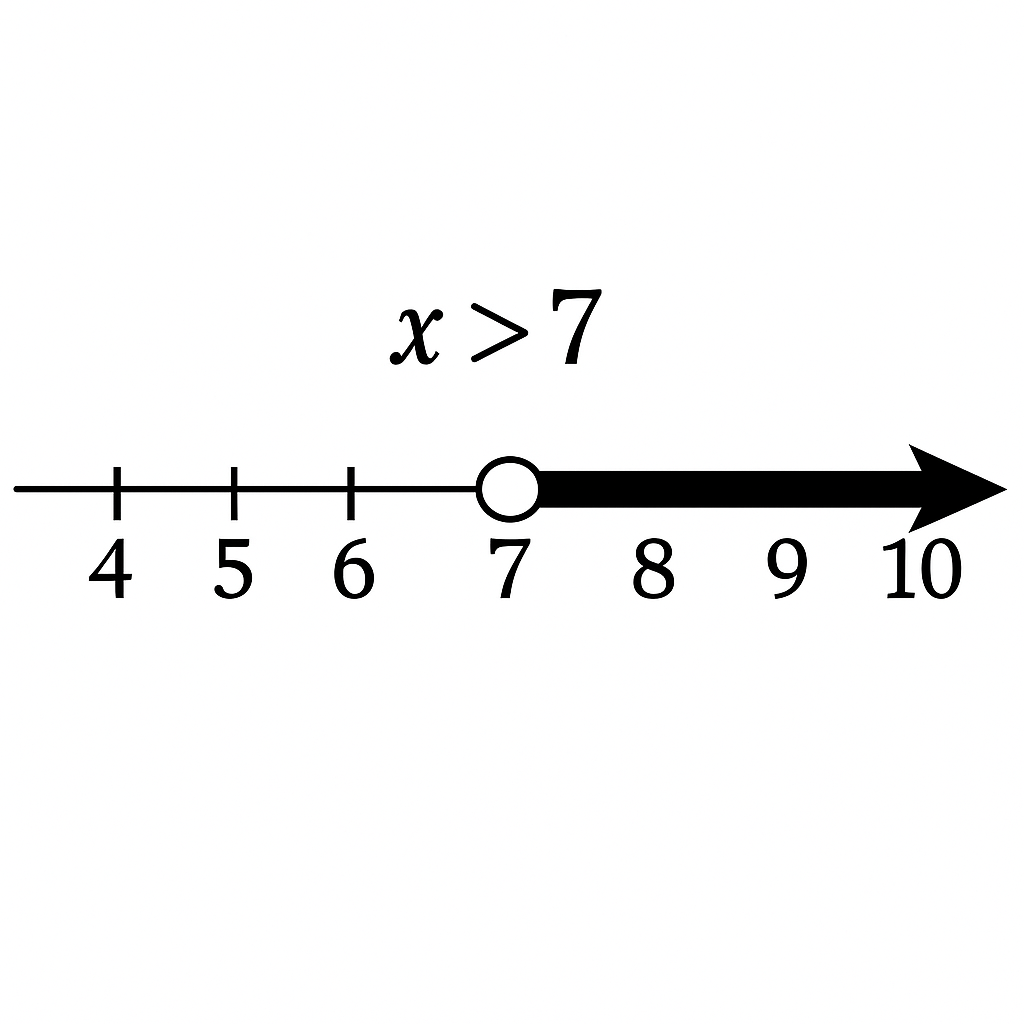
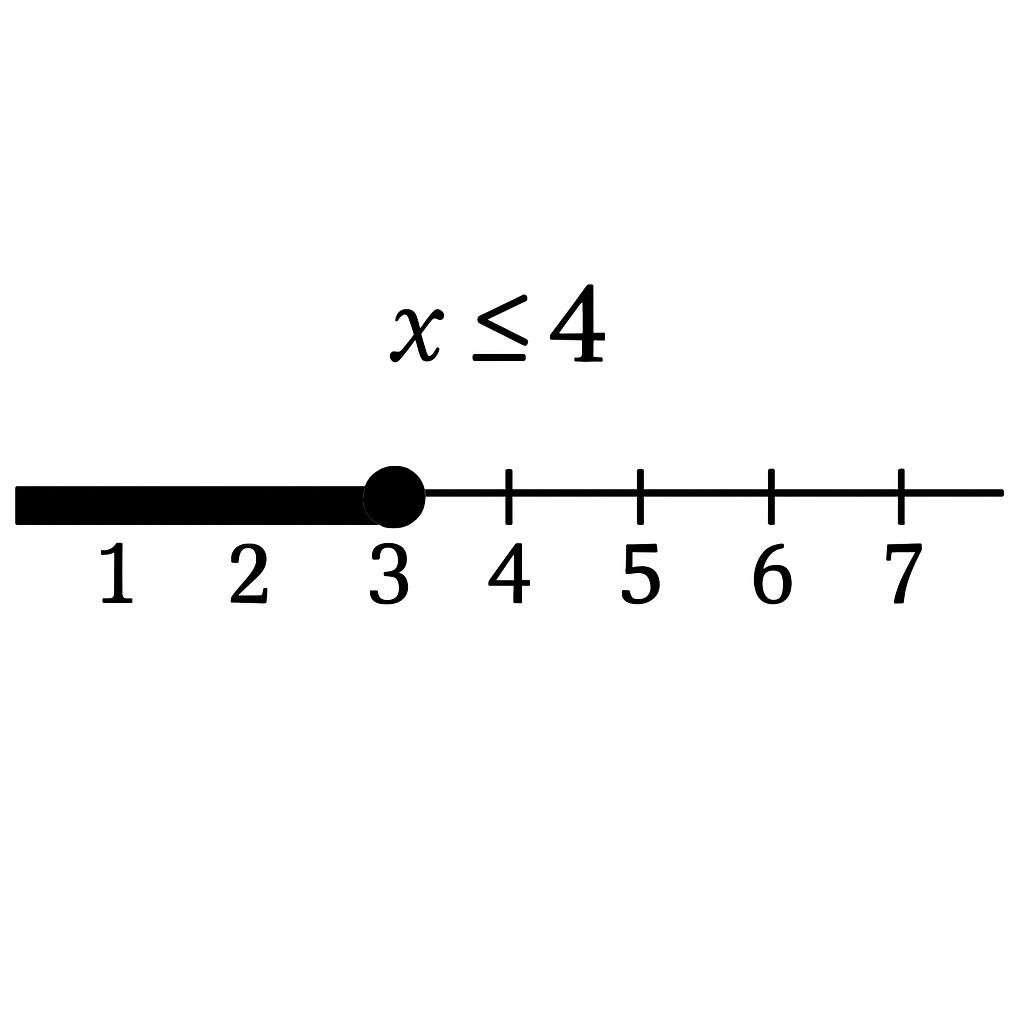
Solve: 2x ≤ 8

Step 1: Divide both sides by 2:

🔹 Example 3: Solving When Dividing by a Negative

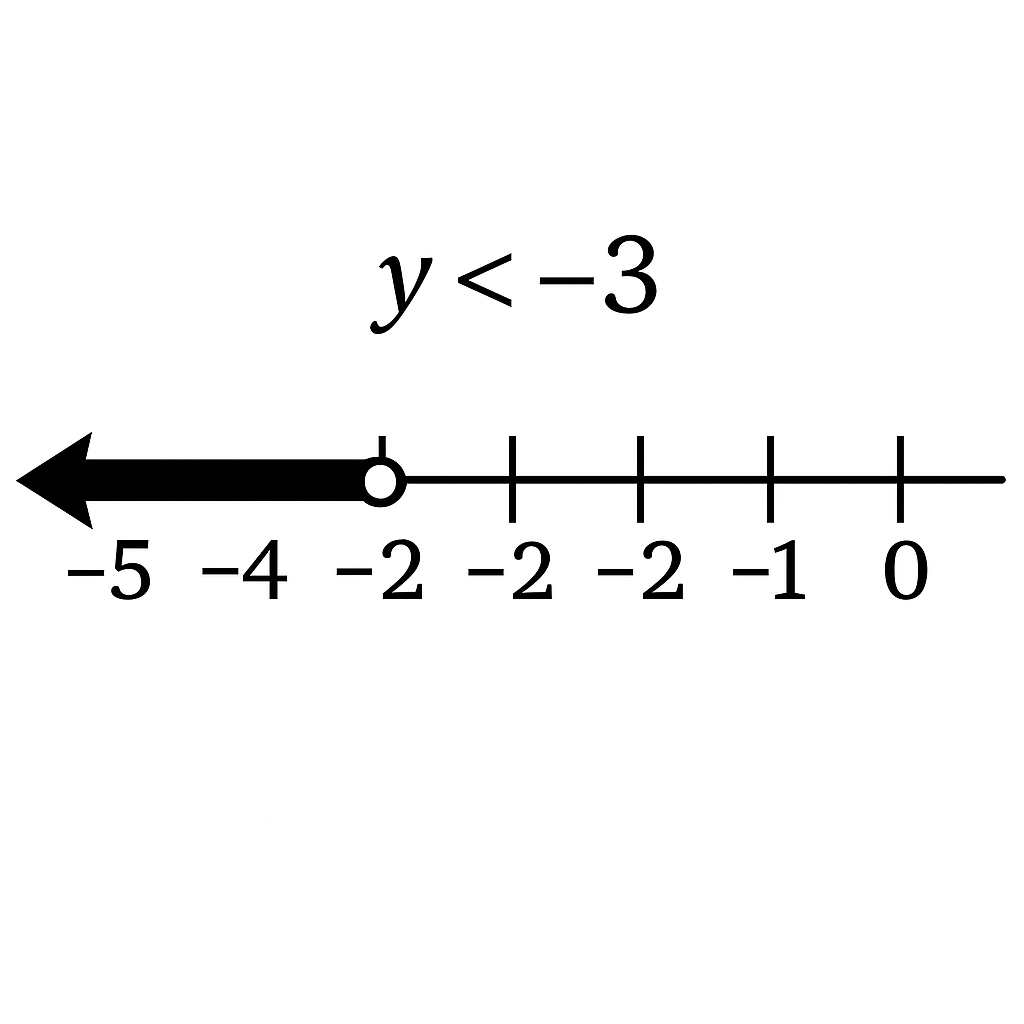
Solve: -3y > 9

Step 1: Divide both sides by -3 and reverse the inequality sign:

📝 Practice Exercises

Practice 1: Solve and Graph

1. x – 4 < 5
2. 2p ≥ 10
3. -2a ≤ 6
4. k/3 > 2

Note: [Leave space to insert number line diagrams after each solution]

Practice 2: True or False

Decide whether these statements are true or false:

1. If you multiply or divide by a negative number, you should reverse the inequality sign. (True/False)
2. x > 5 means x can be 6, 7, or 10. (True/False)

Practice 3: Word Problem Challenge

A bag can carry at most 15 kilograms. If it already holds 8 kilograms, write and solve an inequality to find how much more (w) it can hold.

🔁 Recap

Today you learned:

• Linear inequalities compare two values with >, <, ≥, or ≤.
• You solve them like equations but flip the inequality sign when multiplying or dividing by a negative!
• Solutions are best shown visually on a number line.

🪞 Reflection Prompt

Think about it: If you forget to flip the inequality when dividing by a negative, what kind of mistake could happen?