Lesson 4: Mapping – Functions and Mappings

🟦 Introduction

Welcome! In this lesson, we explore mappings and functions. A mapping shows how each input (from one set) is connected to an output (from another set). When each input has only one output, the mapping is called a function. These ideas are essential in understanding how variables relate in mathematics. Let’s dive in!

🧠 Key Concepts and Explanations

🔹 What is a Mapping?

A mapping is a way of showing a relationship between two sets. Each element in the domain (input) is connected to one or more elements in the codomain (output).

Example: A rule that says “multiply each number by 2” maps 1 to 2, 2 to 4, 3 to 6.

Mapping Table:

🔹 What is a Function?

A function is a special kind of mapping. Each input must map to exactly one output.

• ✅ Allowed: Two inputs can share the same output.
• ❌ Not allowed: One input going to two different outputs.

Example: Input → Multiply by 3

1 → 3, 2 → 6, 3 → 9 — This is a function.

🔹 How Can We Show a Mapping?

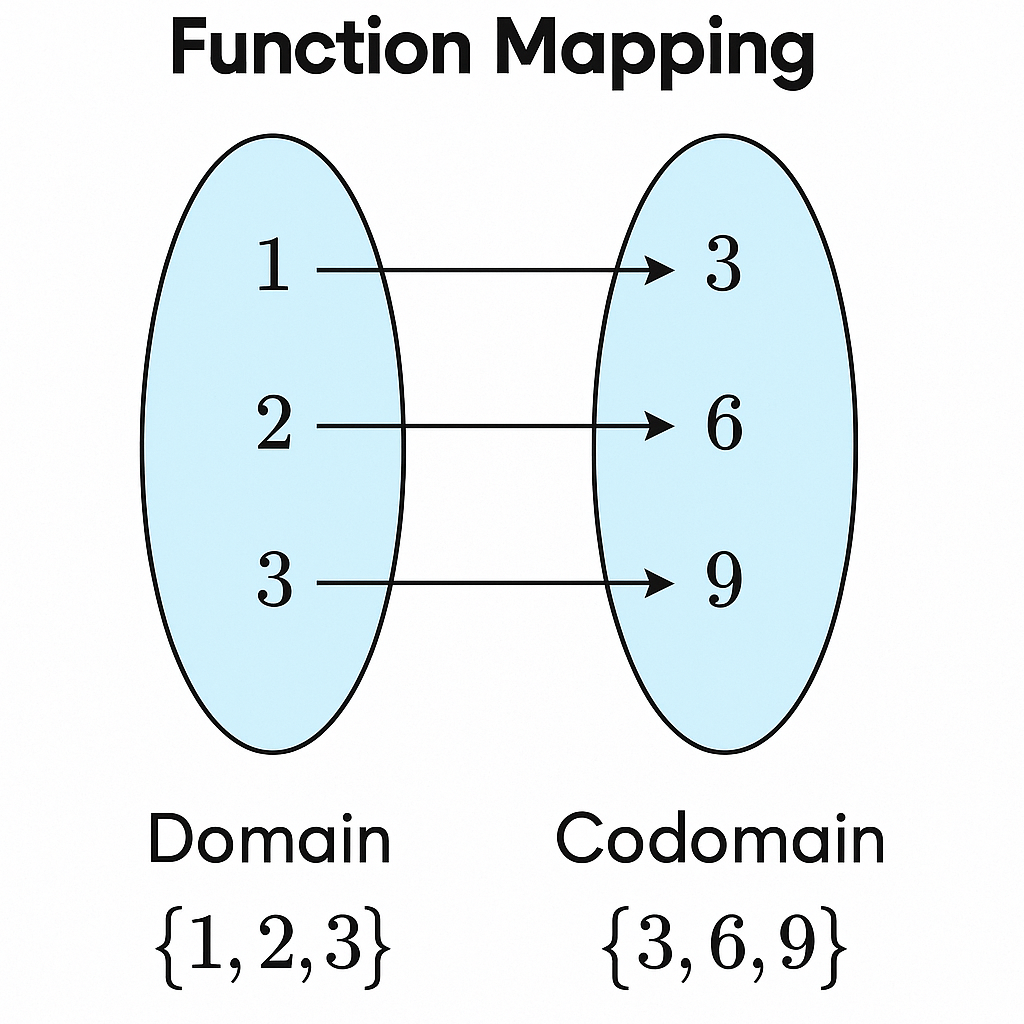
Mappings can be shown in 3 main ways:

• Arrow diagrams — inputs on one side, outputs on the other with arrows.
• Tables — listing pairs of input-output values.
• Ordered pairs — (input, output) written like points.

Example: Rule: Add 4 to each input

Visual: [INSERT ARROW DIAGRAM HERE – Show mapping 1→5, 2→6, 3→7]

🔹 Which Mappings Are NOT Functions?

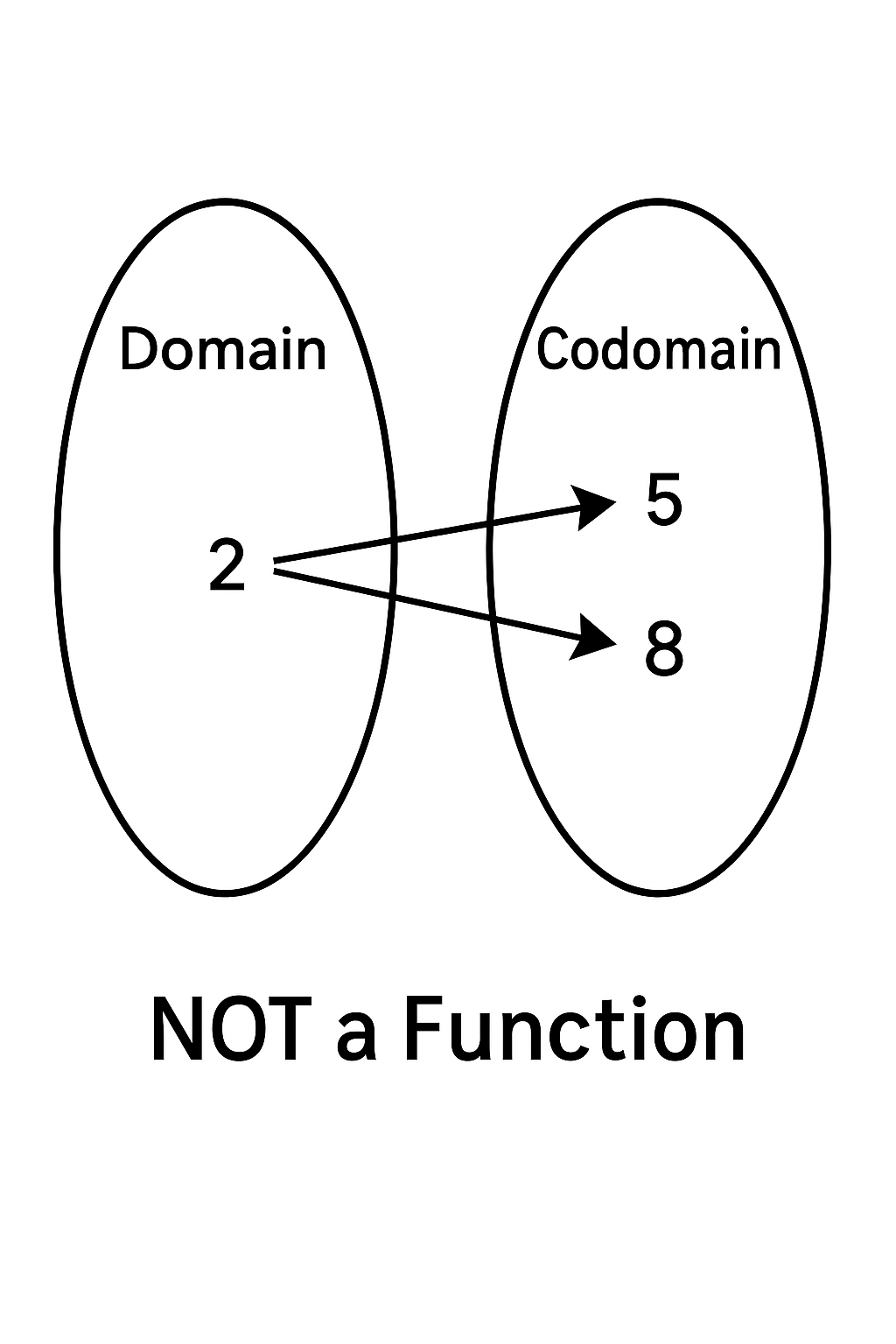
If one input connects to more than one output, the mapping is not a function.

Example: 2 → 5 and 2 → 8 is ❌ NOT a function.

📝 Practice Exercises

Practice 1: Complete the Table

Rule: Subtract 2

Practice 2: Identify Functions

Which of the following are functions?

1. 3 → 7, 4 → 9, 5 → 11
2. 2 → 5, 2 → 8

Practice 3: Word Problem

A machine multiplies each number by 10. If you put in 1, 2, 3, what are the outputs?

🔁 Recap

Today you learned:

• Mappings connect values from a domain to a codomain.
• Functions are mappings where each input has only one output.
• You can show mappings with arrows, tables, or ordered pairs.

🪞 Reflection Prompt

Why do you think functions must connect each input to just one output? What problems might happen if they didn’t?