Lesson 3: Introduction to Sets and Venn Diagrams

👨🏽‍🏫 Introduction

Have you ever made a guest list for a party or grouped your clothes by type (shirts, trousers, shoes)? 🎉👕👟 That’s exactly what we do in Set Theory — we collect and work with groups of related items. In mathematics, a set is a collection of distinct elements that share something in common.

This lesson introduces you to:

• Set notation and types of sets
• Venn diagrams and set relationships
• Operations on sets: union, intersection, complement, and difference
• Solving word problems using Venn diagrams

🧠 Key Concepts

📌 1. What Is a Set?

A set is a collection of well-defined, distinct objects or elements.

We usually write sets using curly braces { }.
Example: The set of vowels = {a, e, i, o, u}

Notation:

• Capital letters (A, B, C) represent sets
• Lowercase letters represent elements (a, b, c)
• means “a is an element of A”
• means “b is not an element of A”

📂 2. Types of Sets

• Finite Set: Set with a countable number of elements (e.g. {1, 2, 3})
• Infinite Set: Goes on forever (e.g. natural numbers)
• Empty Set: Also called null set, has no elements. Notation: { } or ∅
• Universal Set (U): Contains all elements under discussion
• Subset: A set A is a subset of B if every element of A is also in B

📊 3. Venn Diagrams

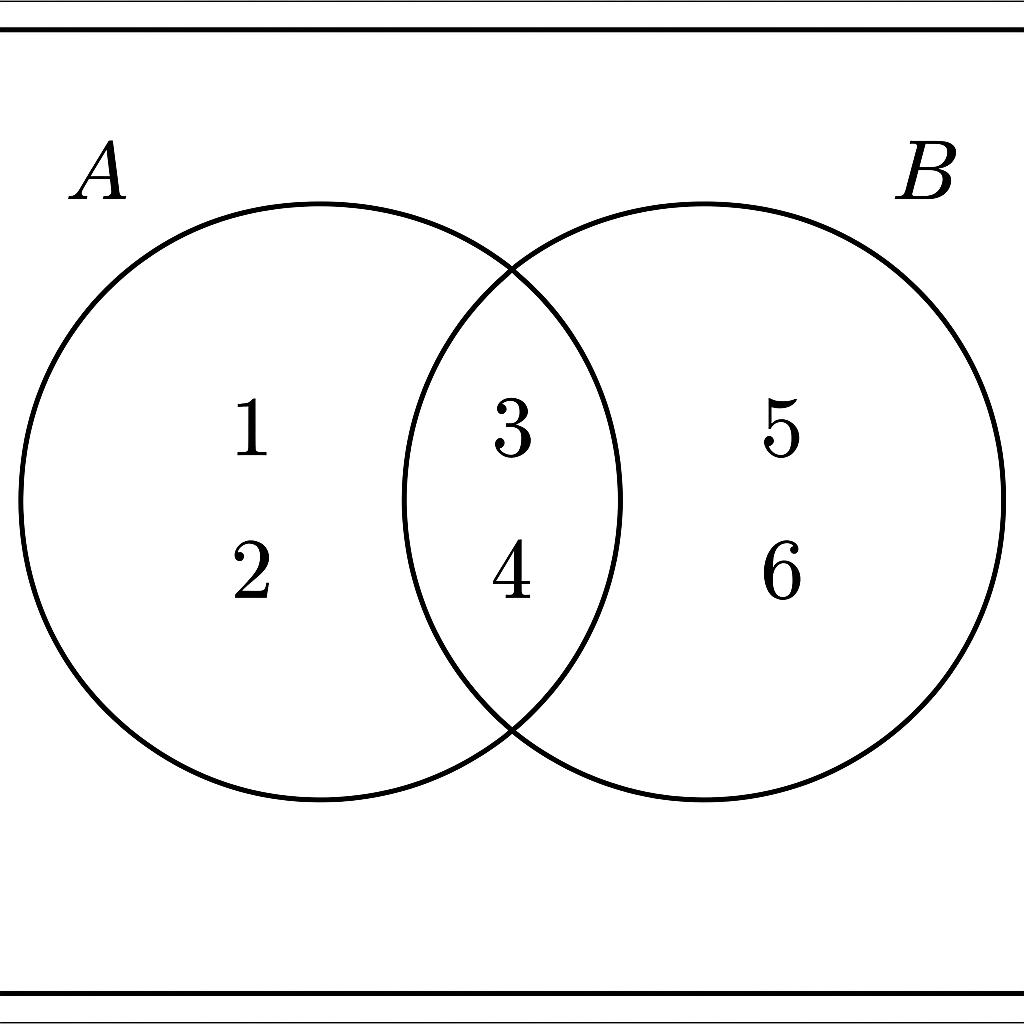
Venn diagrams are used to show the relationship between two or more sets visually. Each set is drawn as a circle. Overlapping areas show shared elements (intersection).

Example:
Let A = {1, 2, 3}, B = {3, 4, 5}
Then the Venn diagram shows 3 in the overlap.

🟢 Set A and 🔵 Set B overlap at element 3.

➕ 4. Operations on Sets

✅ Union (A ∪ B):

All elements in A or B or both.

Example:
A = {1, 2, 3}, B = {3, 4, 5}
A ∪ B = {1, 2, 3, 4, 5}

✅ Intersection (A ∩ B):

Only the elements common to both A and B.

Example:
A ∩ B = {3}

✅ Complement (A′):

All elements in the universal set U that are not in A.

✅ Difference (A – B):

Elements in A but not in B.

Example:
A = {1, 2, 3}, B = {3, 4, 5}
A – B = {1, 2}

🧮 Sample Problem Walkthroughs

1. Let A = {1, 2, 3, 4}, B = {3, 4, 5, 6}. Find A ∪ B and A ∩ B.
   Solution:
   A ∪ B = {1, 2, 3, 4, 5, 6}
   A ∩ B = {3, 4}

   

2. If U = {1, 2, 3, 4, 5, 6}, and A = {2, 4, 6}, find A′.
   Solution:
   A′ = {1, 3, 5}
3. In a class of 40 students, 25 take Maths (M), 18 take English (E), and 10 take both. How many take neither?
   Solution:
   M ∩ E = 10
   M only = 25 – 10 = 15
   E only = 18 – 10 = 8
   Total taking M or E = 15 + 8 + 10 = 33
   So, neither = 40 – 33 = 7

   ---

   ✍🏽 Practice Exercises

   🅰️ A. Basic Set Notation

   1. If A = {2, 4, 6}, B = {4, 6, 8}, find A ∪ B and A ∩ B.
   2. List the elements of A′ if U = {1–10}, A = {2, 4, 6, 8, 10}

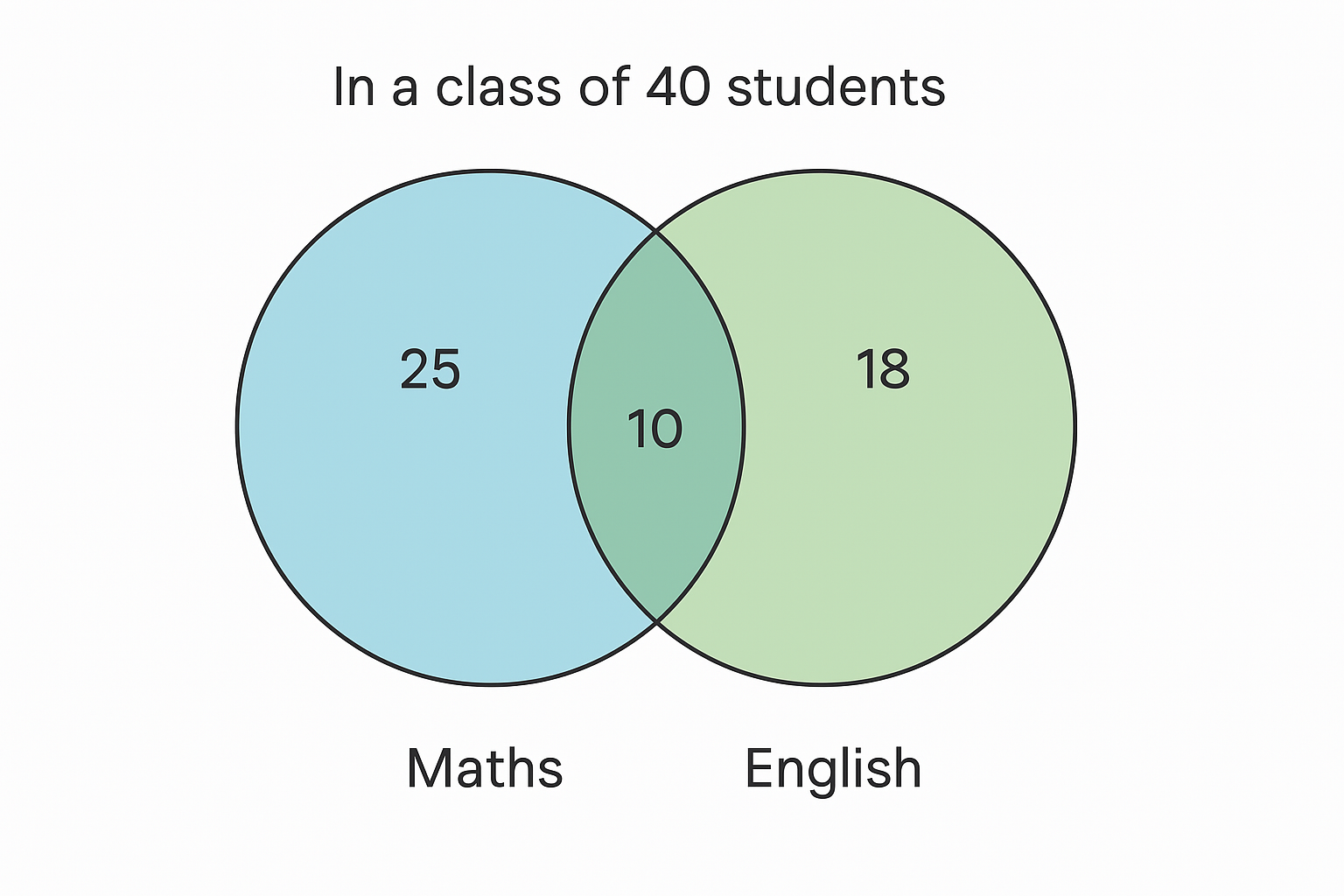
   🅱️ B. Word Problems

   1. In a class of 50 students, 30 take French, 25 take Spanish, and 10 take both. How many take neither?
   2. Let A = {1, 3, 5, 7}, B = {5, 6, 7, 8}. Find A – B and B – A.

   ---

   ✅ Answers and Explanations

   • A1: A ∪ B = {2, 4, 6, 8}, A ∩ B = {4, 6}
   • A2: A′ = {1, 3, 5, 7, 9}
   • B1:
     French only = 30 – 10 = 20
     Spanish only = 25 – 10 = 15
     Total = 20 + 15 + 10 = 45
     Neither = 50 – 45 = 5
   • B2:
     A – B = {1, 3}
     B – A = {6, 8}

   ---

   📌 Recap

   • ✅ A set is a collection of distinct items
   • ✅ Venn diagrams help visualize how sets relate
   • ✅ Key operations: union (∪), intersection (∩), complement (A′), difference (A – B)
   • ✅ Use Venn diagrams to solve word problems involving groups

   ---

   💭 Reflection Prompt

   Think about your own interests — music, sports, books, etc. Could you group them into overlapping sets? Try creating your own Venn diagram with at least 2 categories!